| Definitions | s = t, t  T, x:A T, x:A  B(x), B(x),  x:A. B(x), ES, EState(T), a:A fp x:A. B(x), ES, EState(T), a:A fp B(a), f(a), Id, B(a), f(a), Id, 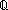 , strong-subtype(A;B), P , strong-subtype(A;B), P   Q, Type, EqDecider(T), Unit, left + right, IdLnk, x:A Q, Type, EqDecider(T), Unit, left + right, IdLnk, x:A  B(x), EOrderAxioms(E; pred?; info), kindcase(k; a.f(a); l,t.g(l;t) ), Knd, loc(e), kind(e), Msg(M), type List, B(x), EOrderAxioms(E; pred?; info), kindcase(k; a.f(a); l,t.g(l;t) ), Knd, loc(e), kind(e), Msg(M), type List,  , val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), r , val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), r  s, e < e', s, e < e',  , ,  b, constant_function(f;A;B), SWellFounded(R(x;y)), b, constant_function(f;A;B), SWellFounded(R(x;y)),  , pred!(e;e'), , pred!(e;e'),   x,y. t(x;y), !Void(), x,y. t(x;y), !Void(), 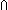 x:A.B(x), Top, S x:A.B(x), Top, S  T, suptype(S; T), first(e), T, suptype(S; T), first(e),  A, <a, b>, pred(e), A, <a, b>, pred(e),  x.A(x), x.A(x),   x. t(x), P & Q, E, AbsInterface(A), e x. t(x), P & Q, E, AbsInterface(A), e   X, {x:A| B(x)} , E(X), sys-antecedent(es;Sys), e c X, {x:A| B(x)} , E(X), sys-antecedent(es;Sys), e c e', let x,y = A in B(x;y), t.1, chain-consistent(f;chain), e', let x,y = A in B(x;y), t.1, chain-consistent(f;chain),  x:A. B(x), P x:A. B(x), P  Q, a < b, hd(l), L1 Q, a < b, hd(l), L1  L2, e L2, e  loc e' , adjacent(T;L;x;y), (x loc e' , adjacent(T;L;x;y), (x  l), no_repeats(T;l), y is f*(x), y=f*(x) via L, ff, inr x , tt, inl x , False, True, case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , X(e), l), no_repeats(T;l), y is f*(x), y=f*(x) via L, ff, inr x , tt, inl x , False, True, case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , X(e),   b, P b, P    Q, p =b q, i <z j, i Q, p =b q, i <z j, i  z j, (i = z j, (i =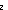 j), x =a y, null(as), a < j), x =a y, null(as), a < b, x f y, a < b, x f y, a < b, [d] b, [d] , eq_atom$n(x;y), q_le(r;s), q_less(a;b), qeq(r;s), a = b, a = b, deq-member(eq;x;L), e = e', p , eq_atom$n(x;y), q_le(r;s), q_less(a;b), qeq(r;s), a = b, a = b, deq-member(eq;x;L), e = e', p    q, p q, p   q, p q, p   q, {T}, SQType(T), s ~ t, last(L), loc(e), n+m, ||as||, #$n, Atom$n, kind(e), first(e), (e <loc e'), source(l), destination(l), es-init(es;e), P q, {T}, SQType(T), s ~ t, last(L), loc(e), n+m, ||as||, #$n, Atom$n, kind(e), first(e), (e <loc e'), source(l), destination(l), es-init(es;e), P   Q, isrcv(e), es-first-from(es;e;l;tg), isrcv(k), lastchange(x;e), (last change to x before e), Q, isrcv(e), es-first-from(es;e;l;tg), isrcv(k), lastchange(x;e), (last change to x before e),  T, locl(a), x T, locl(a), x  dom(f), Dec(P), b | a, a ~ b, a dom(f), Dec(P), b | a, a ~ b, a  b, a <p b, a < b, A c b, a <p b, a < b, A c B, B,  x x L. P(x), ( L. P(x), ( x x L.P(x)), r < s, q-rel(r;x), Outcome, l_disjoint(T;l1;l2), (e < e'), L.P(x)), r < s, q-rel(r;x), Outcome, l_disjoint(T;l1;l2), (e < e'),  e<e'.P(e), e<e'.P(e),  e e e'.P(e), e'.P(e),  e<e'. P(e), e<e'. P(e),  e e e'.P(e), e'.P(e),  e e [e1,e2).P(e), [e1,e2).P(e),  e e [e1,e2).P(e), [e1,e2).P(e),  e e [e1,e2].P(e), [e1,e2].P(e),  e e [e1,e2].P(e), [e1,e2].P(e),  e e (e1,e2].P(e), MaName, (e1,e2].P(e), MaName,  , [car / cdr], [], increasing(f;k), , [car / cdr], [], increasing(f;k),  e e (e1,e2].P(e), @e(x (e1,e2].P(e), @e(x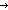 v), pred(e), sender(e), f(x)?z, f**(e), SqStable(P), a =!x:T. Q(x), InvFuns(A;B;f;g), Inj(A;B;f), IsEqFun(T;eq), Refl(T;x,y.E(x;y)), Sym(T;x,y.E(x;y)), Trans(T;x,y.E(x;y)), AntiSym(T;x,y.R(x;y)), Connex(T;x,y.R(x;y)), CoPrime(a,b), Ident(T;op;id), Assoc(T;op), Comm(T;op), Inverse(T;op;id;inv), BiLinear(T;pl;tm), IsBilinear(A;B;C;+a;+b;+c;f), IsAction(A;x;e;S;f), Dist1op2opLR(A;1op;2op), fun_thru_1op(A;B;opa;opb;f), FunThru2op(A;B;opa;opb;f), Cancel(T;S;op), monot(T;x,y.R(x;y);f), IsMonoid(T;op;id), IsGroup(T;op;id;inv), IsMonHom{M1,M2}(f), a v), pred(e), sender(e), f(x)?z, f**(e), SqStable(P), a =!x:T. Q(x), InvFuns(A;B;f;g), Inj(A;B;f), IsEqFun(T;eq), Refl(T;x,y.E(x;y)), Sym(T;x,y.E(x;y)), Trans(T;x,y.E(x;y)), AntiSym(T;x,y.R(x;y)), Connex(T;x,y.R(x;y)), CoPrime(a,b), Ident(T;op;id), Assoc(T;op), Comm(T;op), Inverse(T;op;id;inv), BiLinear(T;pl;tm), IsBilinear(A;B;C;+a;+b;+c;f), IsAction(A;x;e;S;f), Dist1op2opLR(A;1op;2op), fun_thru_1op(A;B;opa;opb;f), FunThru2op(A;B;opa;opb;f), Cancel(T;S;op), monot(T;x,y.R(x;y);f), IsMonoid(T;op;id), IsGroup(T;op;id;inv), IsMonHom{M1,M2}(f), a  b, IsIntegDom(r), IsPrimeIdeal(R;P), f b, IsIntegDom(r), IsPrimeIdeal(R;P), f  g, as @ bs, i g, as @ bs, i 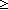 j j |
| Lemmas | adjacent-to-last, adjacent wf, sublist-same-last, decidable es-causle, fun-connected-causle, es-le-causle, es-causle-le, sq stable from decidable, fun-connected-step, decidable equal es-E-interface, es-causl wf, es-locl wf, length wf1, decidable equal Id, decidable assert, fun-connected-induction, implies functionality wrt iff, eq id wf, assert-eq-id, squash wf, es-isrcv-loc, Id sq, iff wf, rev implies wf, es-le-loc, es-le wf, es-loc-pred, es-first wf, null wf3, last wf, es-loc wf, bool cases, eqtt to assert, guard wf, bool sq, iff transitivity, eqff to assert, assert of bnot, bnot wf, es-interface-val wf2, es-interface-val wf, true wf, false wf, btrue wf, bfalse wf, fun-path wf, fun-connected wf, chain-consistent wf, es-E-interface-subtype rel, es-causle wf, sys-antecedent wf, es-interface wf, es-E-interface wf, es-is-interface wf, es-E wf, deq wf, EOrderAxioms wf, kind wf, Msg wf, nat wf, val-axiom wf, cless wf, qle wf, bool wf, Knd wf, kindcase wf, IdLnk wf, constant function wf, loc wf, not wf, assert wf, first wf, top wf, unit wf, pred! wf, strongwellfounded wf, member wf, rationals wf, Id wf, EState wf, subtype rel wf, event system wf |